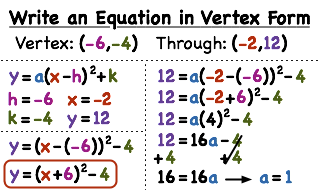What is a parabola? Parabola is a U-shaped symmetrical curve. Its main property is that every point lying on the parabola is in an equal distance to a certain point, called the focus of a parabola, and a line, called its directrix. It is also the curve that corresponds to quadratic equations. The axis of symmetry of a parabola is always perpendicular to the directrix and goes through the focus point. The vertex of a parabola is the point at which the parabola makes the hardest turn; it lies halfway between the focus and the directrix.
Parabola in standard form. Parabola in standard form. An online calculator to find x and y intercepts, find vertex focus and graph the quadratic function. Free quadratic equation calculator - Solve quadratic equations using factoring, complete the square and the quadratic formula step-by-step. Free math problem solver answers your algebra, geometry. Step-by-Step Examples. Conic Sections. Find the Standard Form of the Parabola.
Driver Convertitore Usb Seriale Rs232. A real-life example of a parabola is the path traced by an object in. The parabola equation in vertex form The standard form of the quadratic equation is y = ax² + bx + c. You can use this vertex calculator to transform it to the vertex form that allows you to find the important points of the parabola - vertex and focus. The equation of a parabola in a vertex form is y = a(x-h)² + k, where: • a is the same as the a coefficient in the standard form, • h is the x-coordinate of the parabola vertex, and • k is the y-coordinate of the parabola vertex.
You can calculate the values of h and k from the equations below: h = - b/(2a) k = c - b²/(4a). Optitex Crack Windows 7 more. How to use the parabola equation calculator: an example • Enter the coefficients a, b and c of the standard form of your quadratic equation.
Let's assume that the equation was y = 2x² + 3x - 4, what makes a = 2, b = 3 and c = -4. • Calculate the coordinates of the vertex, using the formulas listed above: h = - b/(2a) = -3/4 = -0.75 k = c - b²/(4a) = -4 - 9/8 = -5.125 • Find the coordinates of the focus of the parabola. The x-coordinate of the focus is the same as of the vertex (x₀ = -0.75), and the y-coordinate is y₀ = c - (b² - 1)/(4a) = -4 - (9-1)/8 = -5 • Find the directrix of the parabola. You can either use the parabola calculator to do it for you or use the equation y = c - (b² + 1)/(4a) = -4 - (9+1)/8 = -5.25.